Одно из самых интересных и полезных открытий в механике - это закон сохранения энергии. Зная формулы для кинетической и потенциальной энергий механической системы, мы способны обнаруживать связь между состояниями системы в два разных момента времени, не вникая в подробности того, что происходит между этими моментами. Мы хотим определить теперь энергию электростатических систем. В электричестве сохранение энергии окажется столь же полезным для обнаружения многих любопытных фактов.
Закон, по которому меняется энергия при электростатическом взаимодействии, очень прост; на самом деле мы его уже обсуждали. Пусть имеются заряды и , разделенные промежутком . У этой системы есть какая-то энергия, потому что понадобилась какая-то работа, чтобы сблизить заряды. Мы подсчитывали работу, производимую при сближении двух зарядов с большого расстояния; она равна
Мы знаем из принципа наложения, что если зарядов много, то общая сила, действующая на любой из зарядов, равна сумме сил, действующих со стороны всех прочих зарядов. Отсюда следует, что полная энергия системы нескольких зарядов есть сумма членов, выражающих взаимодействие каждой пары зарядов по отдельности. Если и - какие-то два из зарядов, а расстояние между ними (фиг. 8.1), то энергия именно этой пары равна
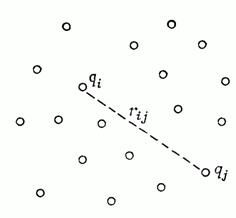
Фигура 8.1. Электростатическая энергия системы частиц есть сумма электростатических энергий каждой пары
Полная электростатическая энергия есть сумма энергий всевозможных пар зарядов:
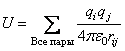 (8.3)
(8.3)
Если распределение задается плотностью заряда , то сумму в (8.3) нужно, конечно, заменить интегралом.
Мы расскажем здесь об энергии с двух точек зрения. Первая - применение понятия энергии к электростатическим задачам; вторая - разные способы оценки величины энергии. Порой легче бывает подсчитать выполненную в каком-то случае работу, чем оценить величину суммы в (8.3) или величину соответствующего интеграла. Для образца подсчитаем энергию, необходимую для того, чтобы собрать из зарядов однородно заряженный шар. Энергия здесь есть не что иное, как работа, которая затрачивается на собирание зарядов из бесконечности.
Представьте, что мы сооружаем шар, наслаивая последовательно друг на друга сферические слои бесконечно малой толщины. На каждой стадии процесса мы собираем небольшое количество электричества и размещаем его тонким слоем от до . Мы продолжаем процесс этот до тех пор, пока не доберемся до заданного радиуса (фиг. 8.2). Если - это заряд шара в тот момент, когда шар доведен до радиуса , то работа, требуемая для доставки на шар заряда , равна
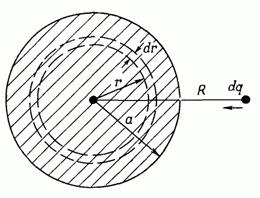
Фигура 8.2. Энергию однородно заряженного шара можно рассчитать, вообразив, что его слепили, последовательно наслаивая друг на друга сферические слои.
Если плотность заряда внутри шара есть , то заряд равен
а заряд равен по всем парам точек внутри шара равно .
7. Энергия электрического поля
(Примеры решения задач)
Энергия взаимодействия зарядов
Пример 1.
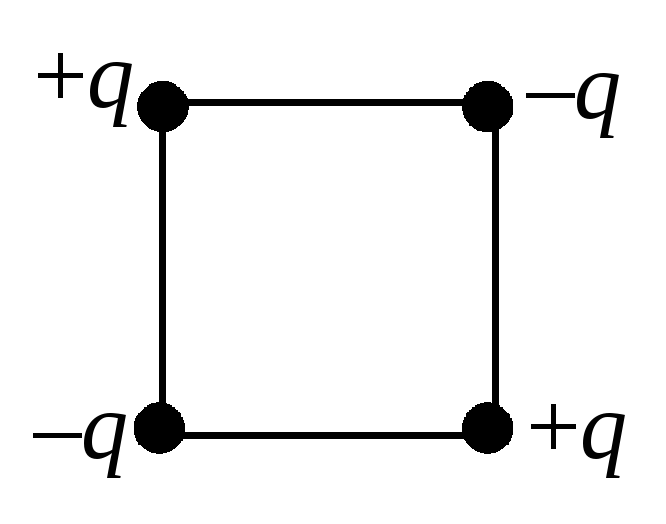
Определите электрическую энергию взаимодействия точечных зарядов, расположенных в вершинах квадрата со стороной a (см. рис.2).
Решение .
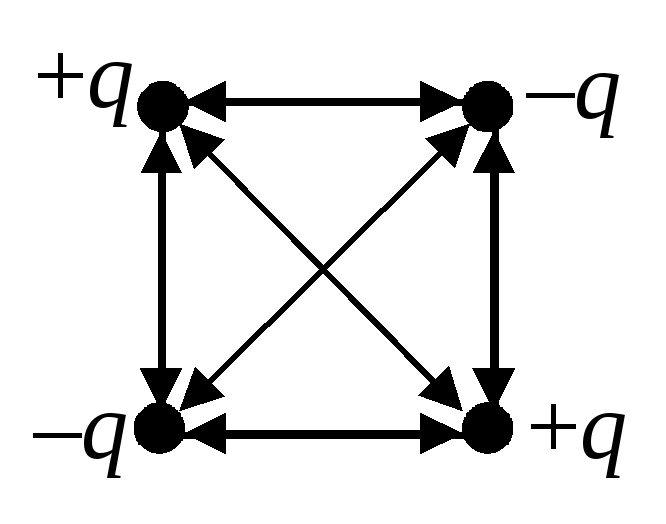
На рис.3 условно изображены двунаправленными стрелками все парные взаимодействия зарядов. Учитывая энергии всех этих взаимодействий, получим:
|
|
|
|
Пример 2.
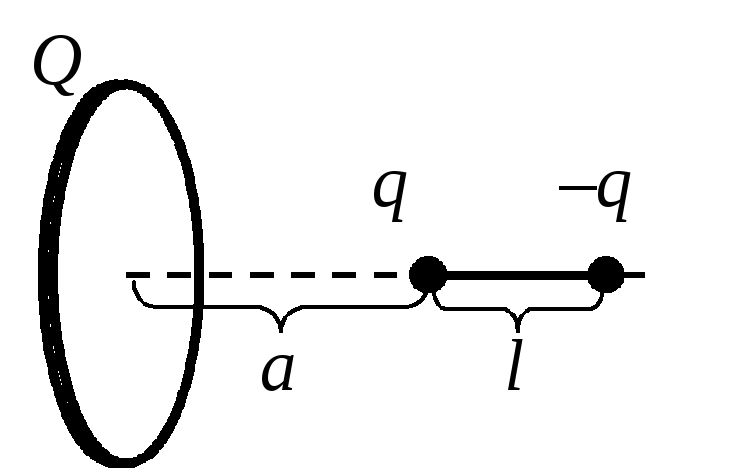
Определите электрическую энергию взаимодействия заряженного кольца с диполем, расположенным на его оси, как показано на рис.4. Известны расстояния a , l , заряды Q , q и радиус кольца R .
Решение .
При решении задачи следует учесть все энергии парных взаимодействий зарядов одного тела (кольца) с зарядами другого тела (диполя). Энергия взаимодействия точечного заряда q с зарядомQ , распределенным по кольцу, определяется суммой
![]() ,
,
где
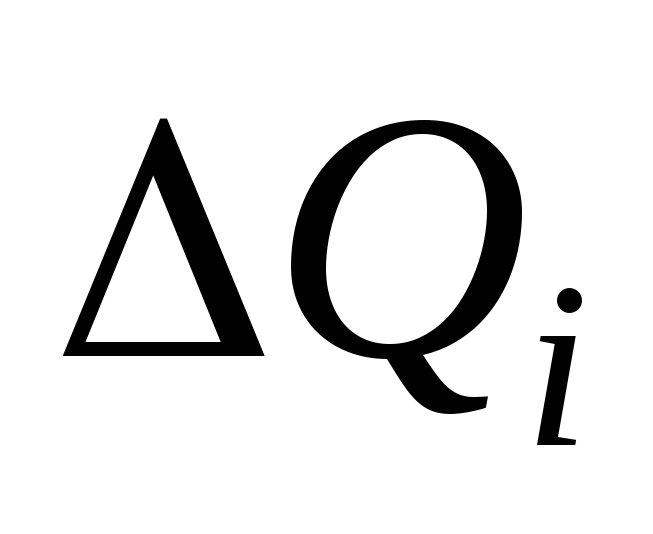 - заряд
бесконечно малого фрагмента кольца,
- заряд
бесконечно малого фрагмента кольца,
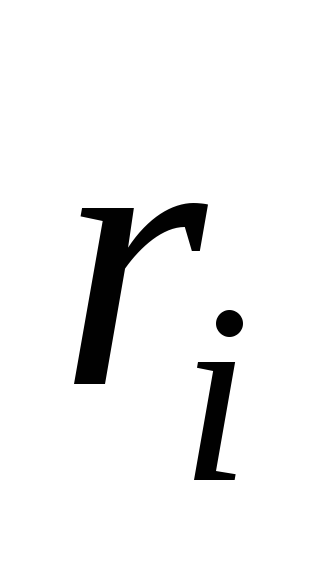 -
расстояние
от этого фрагмента до зарядаq
.
Поскольку все
-
расстояние
от этого фрагмента до зарядаq
.
Поскольку все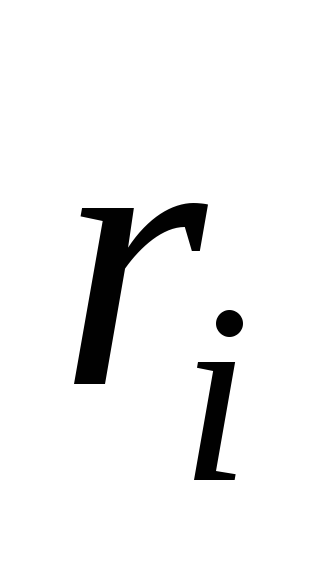 одинаковы и равны
одинаковы и равны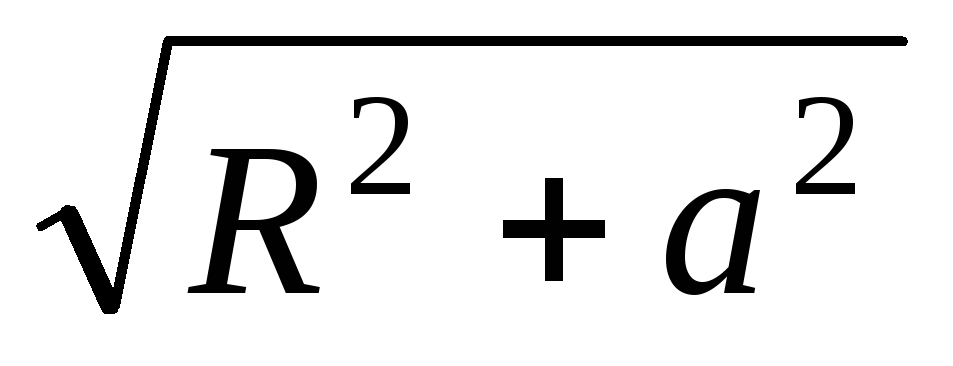 ,
то
,
то
Аналогично найдем энергию взаимодействия точечного заряда –q с заряженным кольцом:
Суммируя W 1 иW 2 , получим для энергии взаимодействия кольца с диполем:
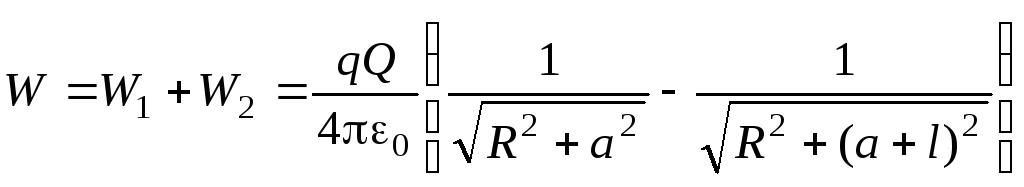 .
.
Электрическая энергия заряженных проводников
Пример 3.
Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q , ее первоначальный радиус R .
Решение .
Электрическая энергия уединенного
проводника определяется формулой
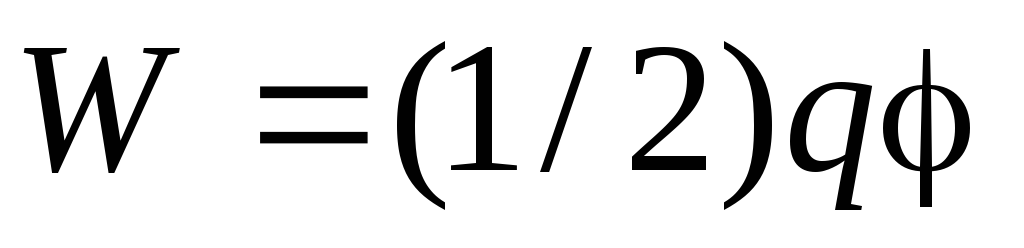 ,
гдеq
–
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаR
равен
,
гдеq
–
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаR
равен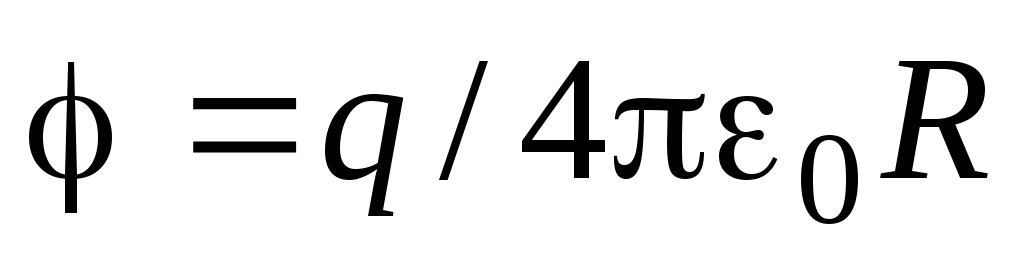 ,
найдем ее электрическую энергию:
,
найдем ее электрическую энергию:
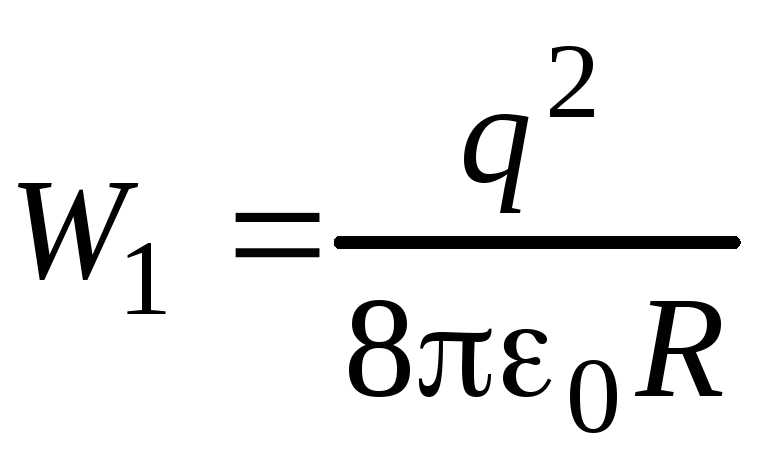 .
.
После уменьшения в два раза радиуса сферы ее энергия становится равной
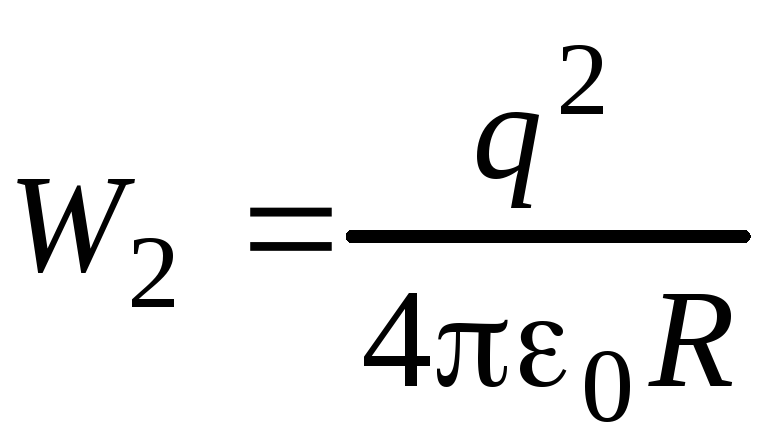 .
.
Электрические силы при этом совершают работу
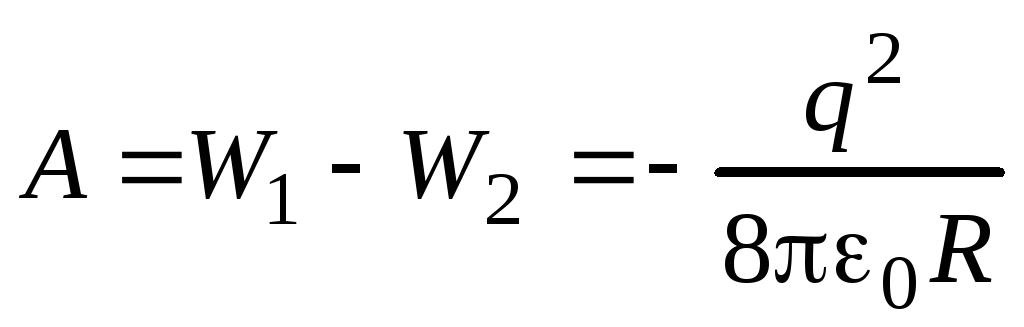 .
.
Пример 4.
Два металлических шара, радиусы которых r и 2r , а соответствующие заряды 2q и –q , расположены в вакууме на большом расстоянии друг от друга. Во сколько раз уменьшится электрическая энергия системы, если шары соединить тонкой проволокой?
Решение .
После соединения шаров тонкой проволокой их потенциалы становятся одинаковыми
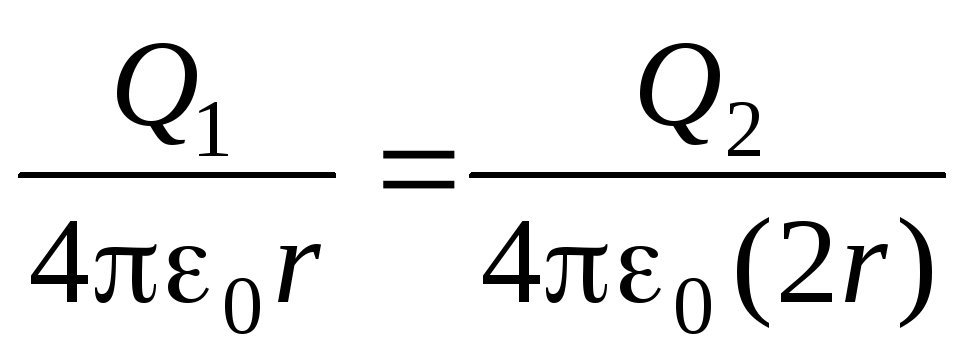 ,
,
а установившиеся заряды шаров Q 1 и Q 2 получаются в результате перетекания заряда с одного шара на другой. При этом суммарный заряд шаров остается постоянным:
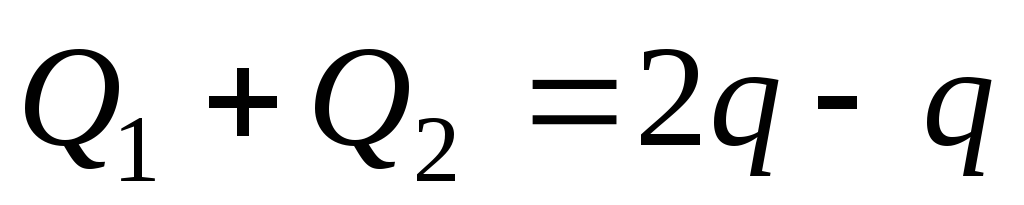 .
.
Из этих уравнений найдем
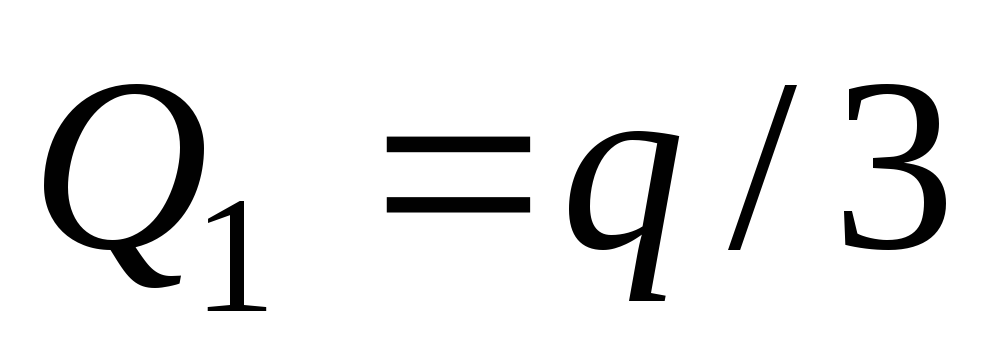 ,
,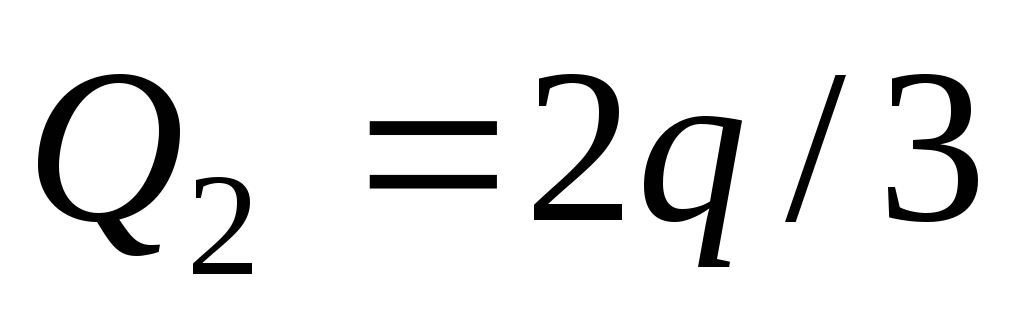 .
.
Энергия шаров до соединения их проволокой равна
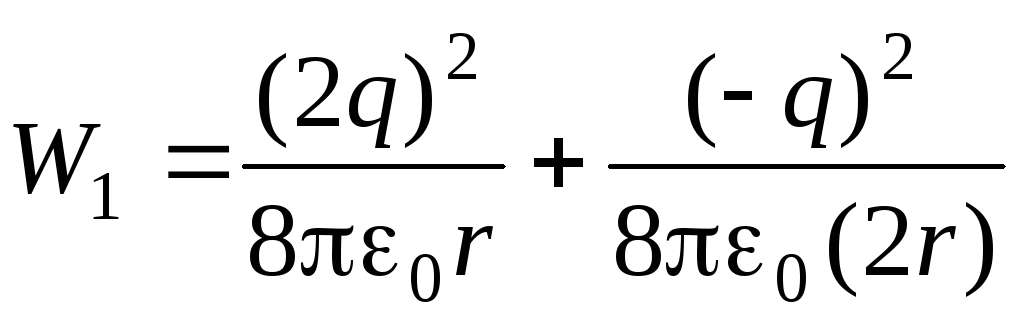 ,
,
а после соединения
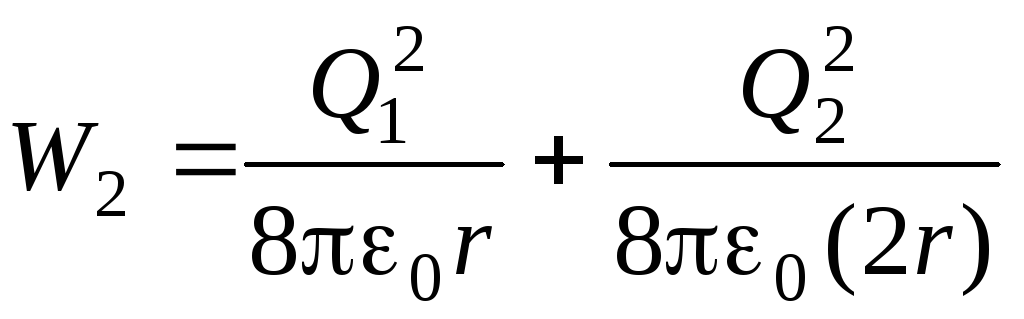 .
.
Подставляя в последнее выражение значения Q 1 и Q 2 , получим после простых преобразований
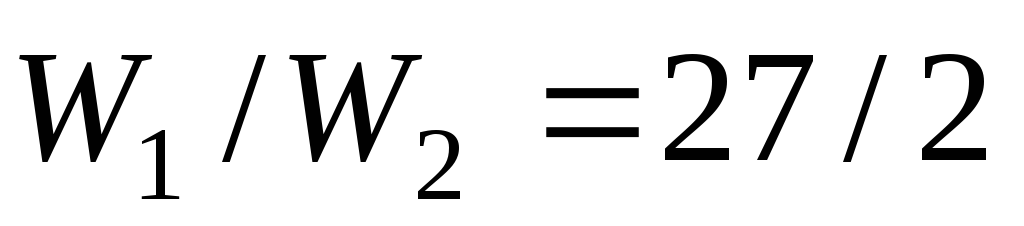 .
.
Пример 5.
В один шар слились N = 8 одинаковых шариков ртути, заряд каждого из которых q . Считая, что в начальном состоянии ртутные шарики находились на большом расстоянии друг от друга, определите, во сколько раз увеличилась электрическая энергия системы.
Решение .
При слиянии ртутных шариков сохраняется их суммарный заряд и объем:
![]() ,
,
где Q – заряд шара, R – его радиус, r – радиус каждого маленького ртутного шарика. Суммарная электрическая энергия N уединенных шариков равна
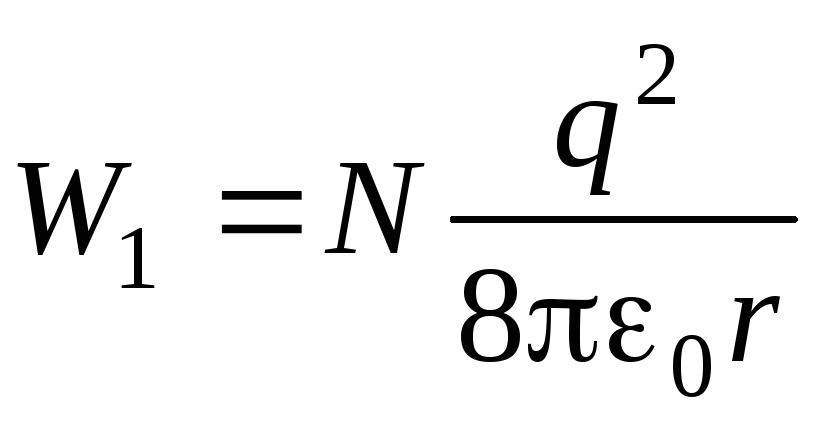 .
.
Электрическая энергия полученного в результате слияния шара
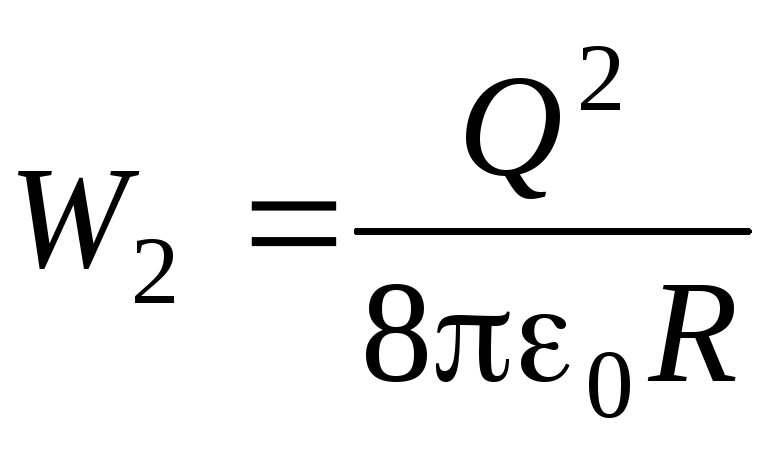 .
.
После алгебраических преобразований получим
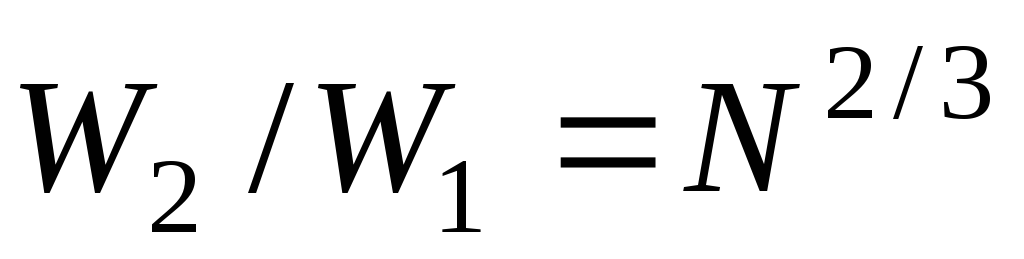 = 4.
= 4.
Пример 6.
Металлический шарик радиуса R = 1 мм и заряда q = 0,1 нКл с большого расстояния медленно приближают к незаряженному проводнику и останавливают, когда потенциал шарика становится равным = 450 В. Какую работу для этого следует совершить?
Решение .
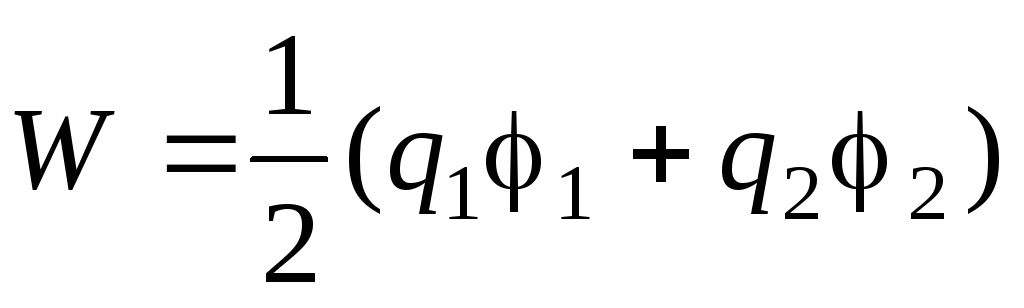 ,
,
где q 1 иq 2 – заряды проводников, 1 и 2 – их потенциалы. Так как проводник по условию задачи не заряжен, то
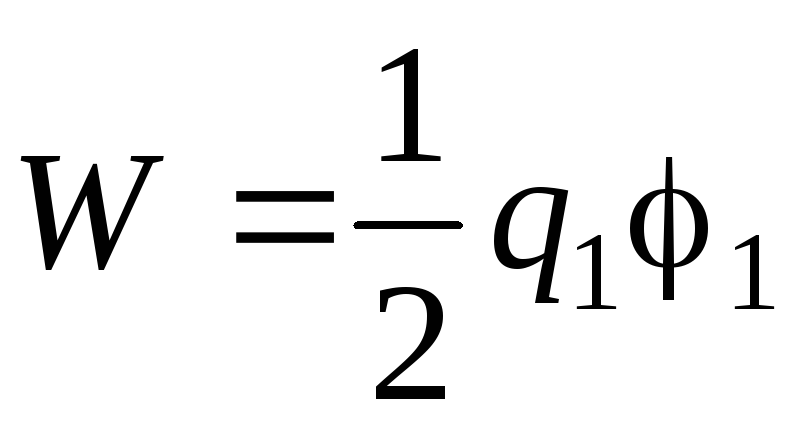 ,
,
где q 1 и 1 заряд и потенциал шара. Когда шар и незаряженный проводник находятся на большом расстоянии друг от друга,
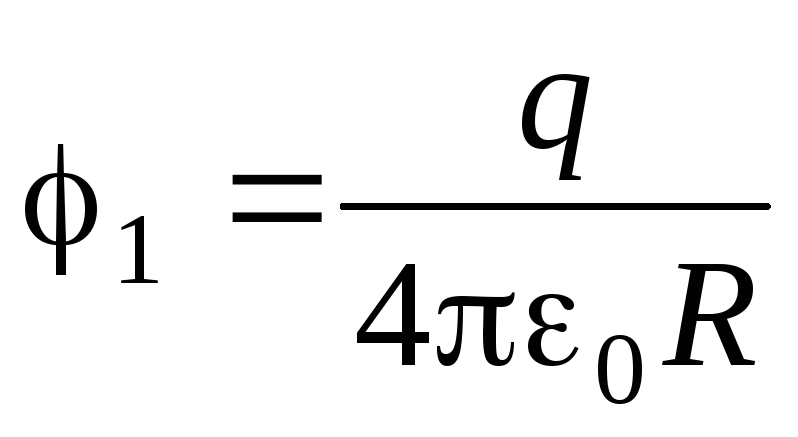 ,
,
и электрическая энергия системы
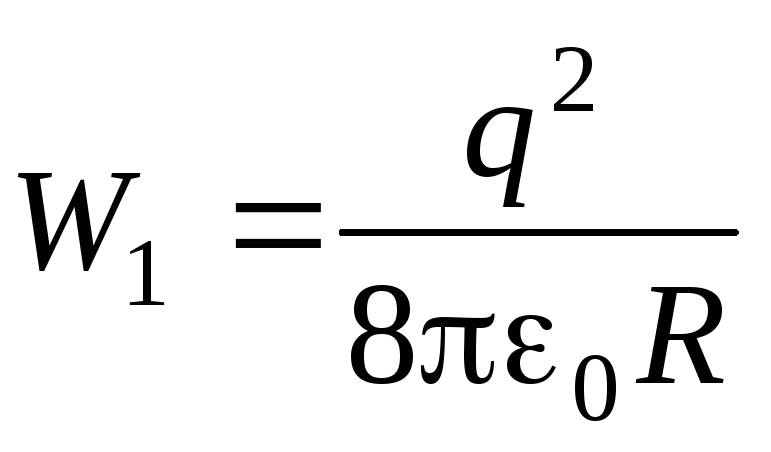 .
.
В конечном состоянии системы, когда потенциал шара стал равным , электрическая энергия системы:
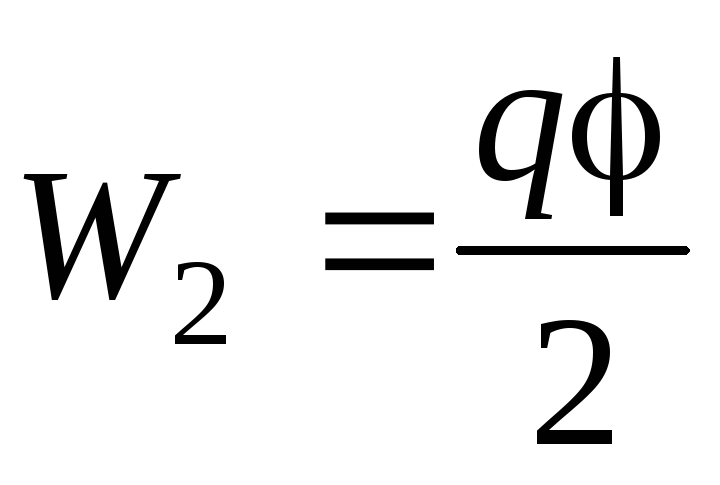 .
.
Работа внешних сил равна приращению электрической энергии:
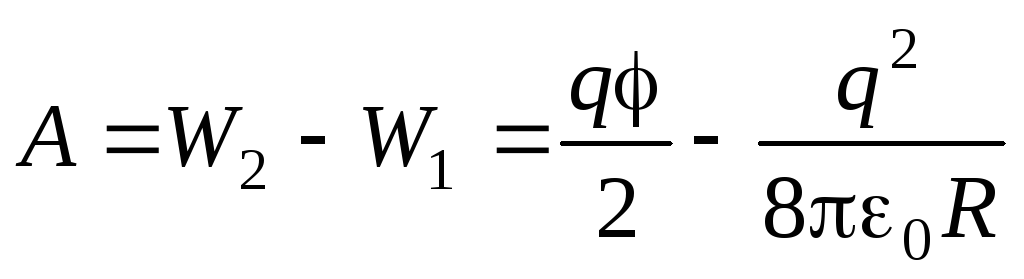 = –0,0225 мкДж.
= –0,0225 мкДж.
Заметим, что электрическое поле в конечном состоянии системы создается зарядами, индуцированными на проводнике, а также зарядами, неоднородно распределенными по поверхности металлического шара. Рассчитать это поле при известной геометрии проводника и заданном положении металлического шара весьма непросто. Нам не потребовалось этого делать, поскольку в задаче задана не геометрическая конфигурация системы, а потенциал шара в конечном состоянии.
Пример 7 .
Система состоит
из двух концентрических тонких
металлических оболочек с радиусами R
1
и R
2
(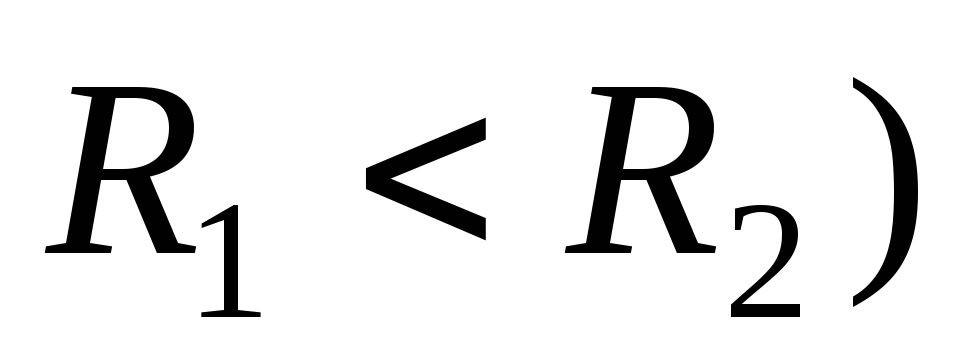 и
соответствующими зарядамиq
1
и q
2 .
Найдите электрическую энергию W
системы. Рассмотрите также специальный
случай, когда
и
соответствующими зарядамиq
1
и q
2 .
Найдите электрическую энергию W
системы. Рассмотрите также специальный
случай, когда
![]() .
.
Решение .
Электрическая энергия системы из двух заряженных проводников определяется формулой
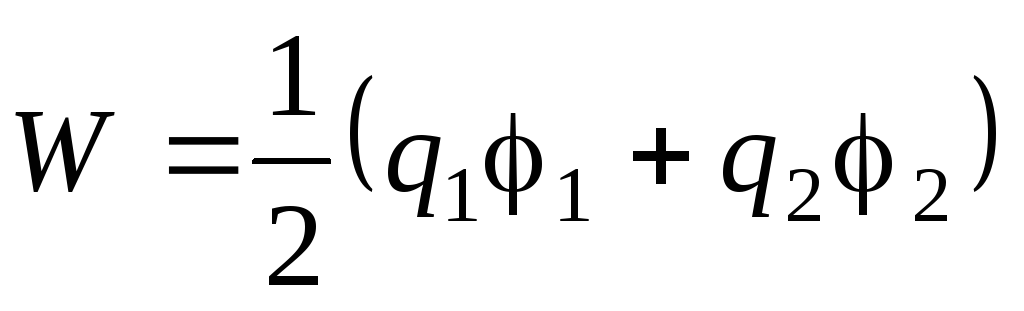 .
.
Для решения задачи необходимо найти потенциалы внутренней ( 1) и внешней ( 2) сфер. Это нетрудно сделать (см. соответствующий раздел пособия):
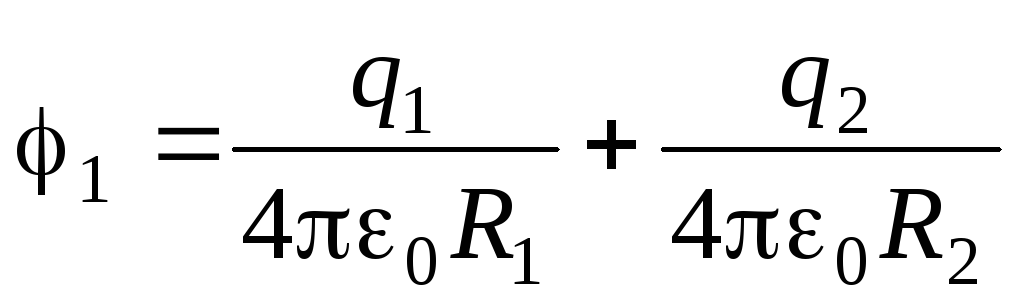 ,
,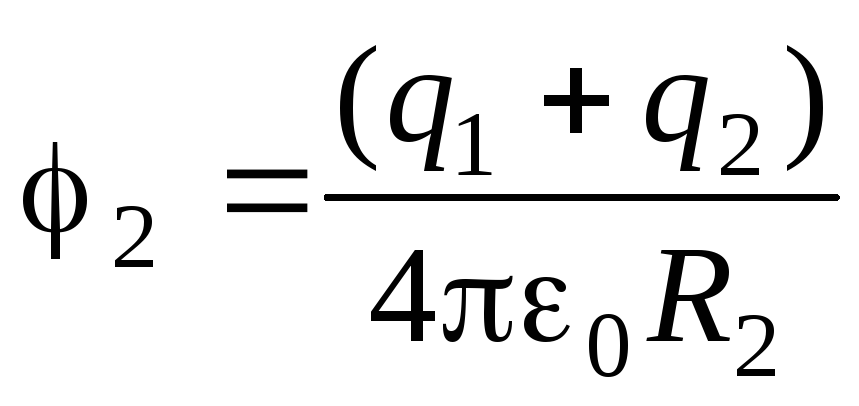 .
.
Подставляя эти выражения в формулу для энергии, получим
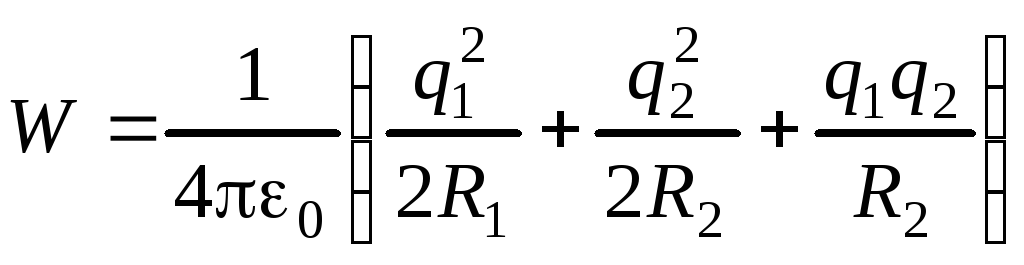 .
.
При
![]() энергия равна
энергия равна
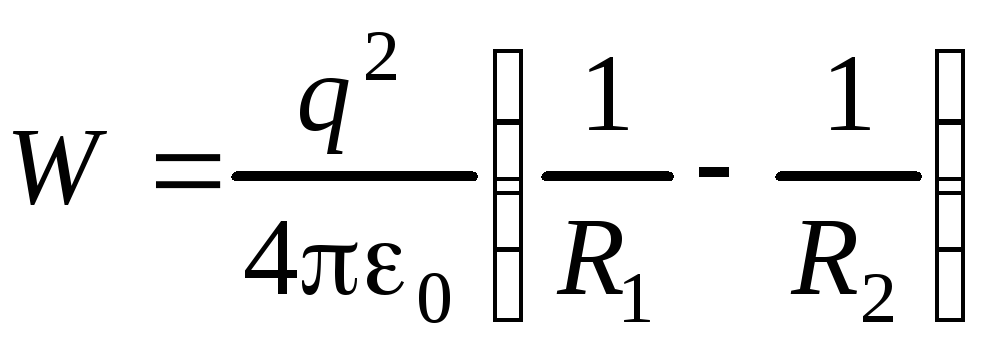 .
.
Собственная электрическая энергия и энергия взаимодействия
Пример 8.
Две проводящие сферы, заряды которых q и –q , радиусы R 1 и R 2 , расположены в вакууме на большом расстоянии друг от друга. Сфера большего радиуса R 2 состоит из двух полусфер. Полусферы разъединяют, подносят их к сфере радиуса R 1 , и вновь соединяют, образуя таким образом сферический конденсатор. Определите работу электрических сил при таком составлении конденсатора.
Решение .
Электрическая энергия двух удаленных друг от друга заряженных сфер равна
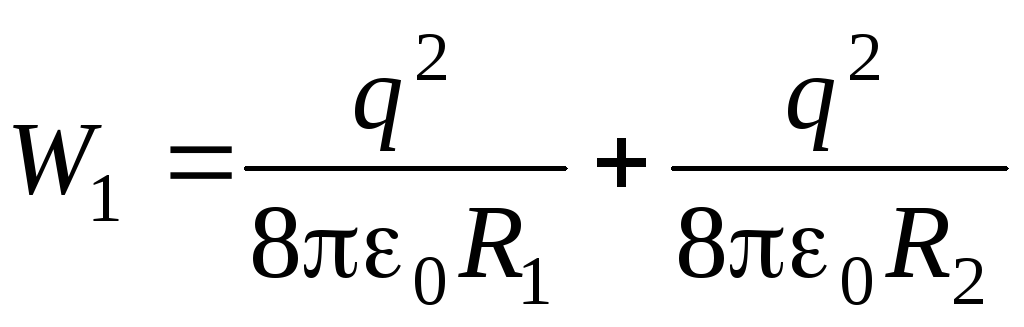 .
.
Электрическая энергия полученного сферического конденсатора:
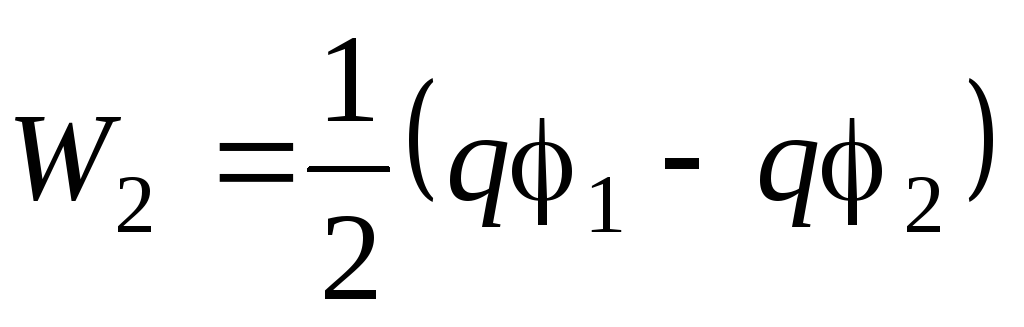 ,
,
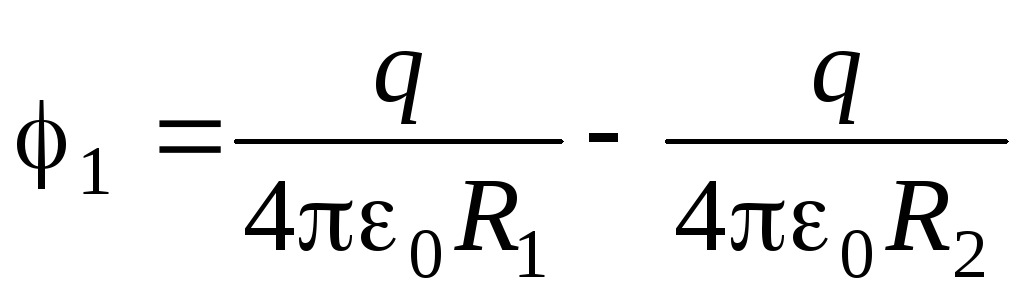
Потенциал
внутренней сферы,
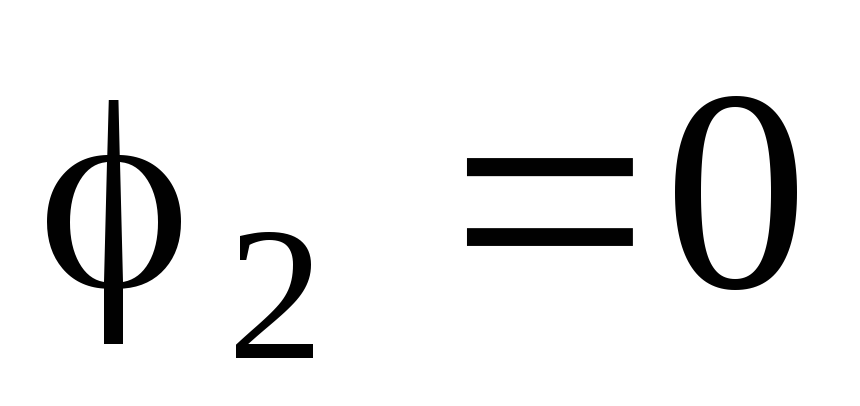 - потенциал внешней сферы. Следовательно,
- потенциал внешней сферы. Следовательно,
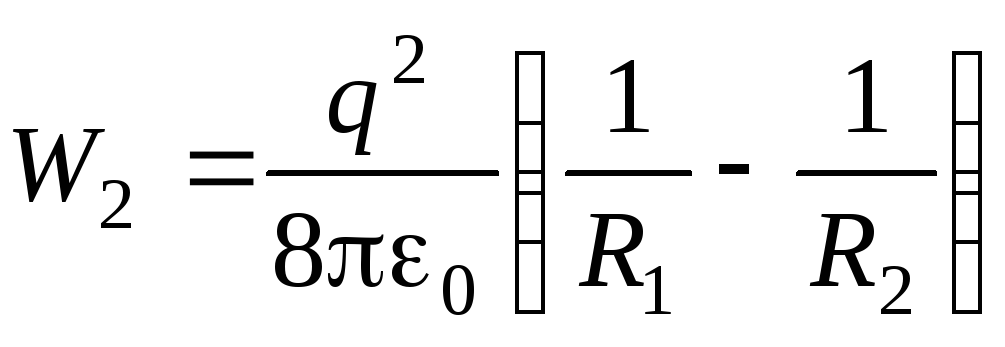
Работа электрических сил при таком составлении конденсатора:
Заметим, что
электрическая энергия сферического
конденсатора W
2
равна работе внешних
сил по зарядке конденсатора. При этом
электрические силы совершают работу
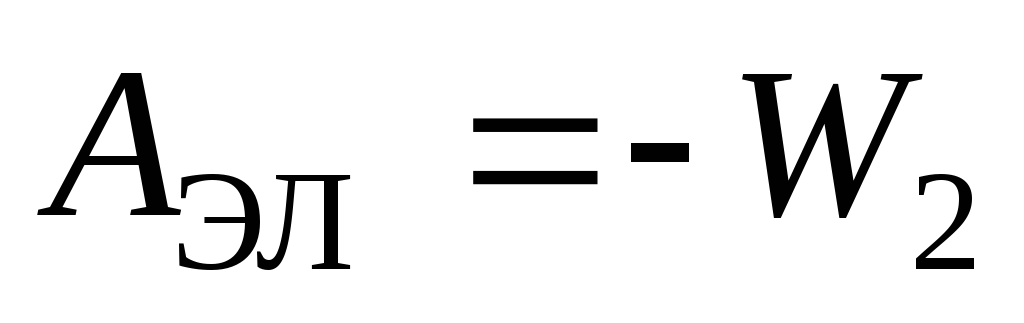 .
Эта работа совершается не только при
сближении заряженных обкладок, но и при
нанесении заряда на каждую из обкладок.
ПоэтомуA
ЭЛ
отличается от найденной выше работы A
,
совершенной электрическими силами
только при сближения обкладок.
.
Эта работа совершается не только при
сближении заряженных обкладок, но и при
нанесении заряда на каждую из обкладок.
ПоэтомуA
ЭЛ
отличается от найденной выше работы A
,
совершенной электрическими силами
только при сближения обкладок.
Пример 9.
Точечный заряд q = 1,5 мкКл расположен в центре сферической оболочки, по поверхности которой однородно распределен заряд Q = 5 мкКл. Найдите работу электрических сил при расширении оболочки – увеличении ее радиуса от R 1 = 50 мм до R 2 = 100 мм.
Решение .
Энергия взаимодействия точечного заряда q с зарядами, расположенными на сферической оболочке радиуса R равна
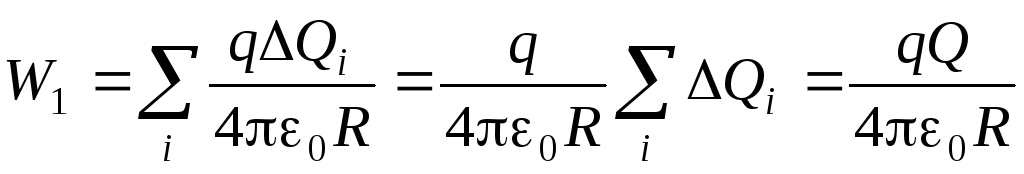 ,
,
Собственная электрическая энергия оболочки (энергия взаимодействия зарядов оболочки между собой) равна:
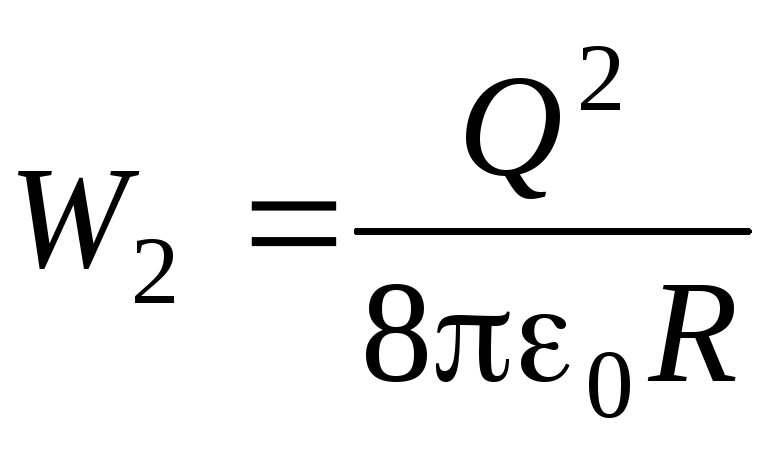 .
.
Работа электрических сил при расширении оболочки:
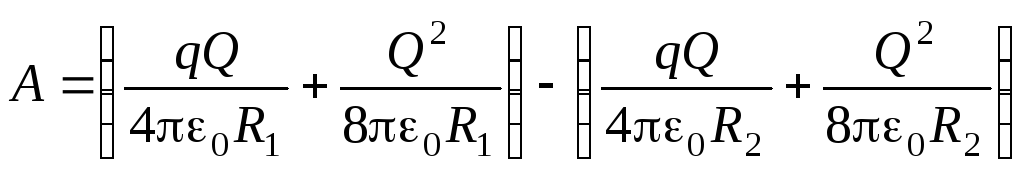 .
.
После преобразований получим
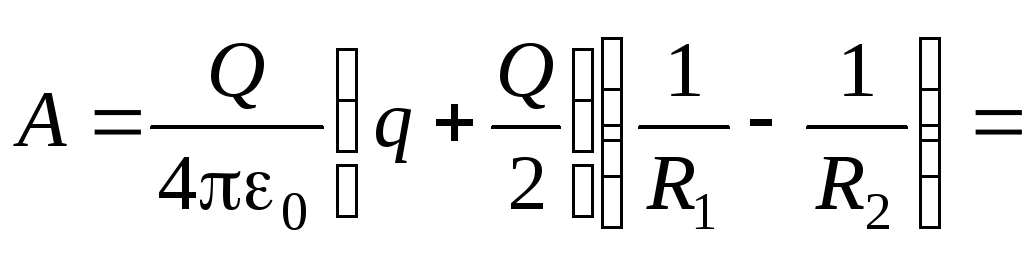 1,8 Дж.
1,8 Дж.
Другой способ решения
Точечный заряд представим в виде однородно заряженной сферы малого радиуса r и заряда q . Полная электрическая энергия системы равна
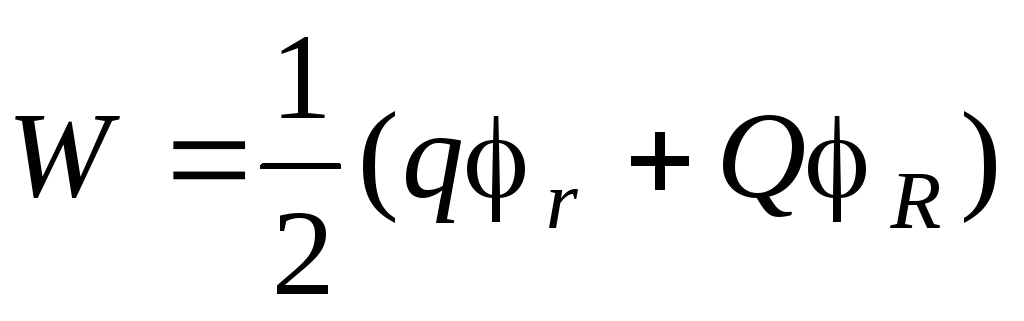 ,
,
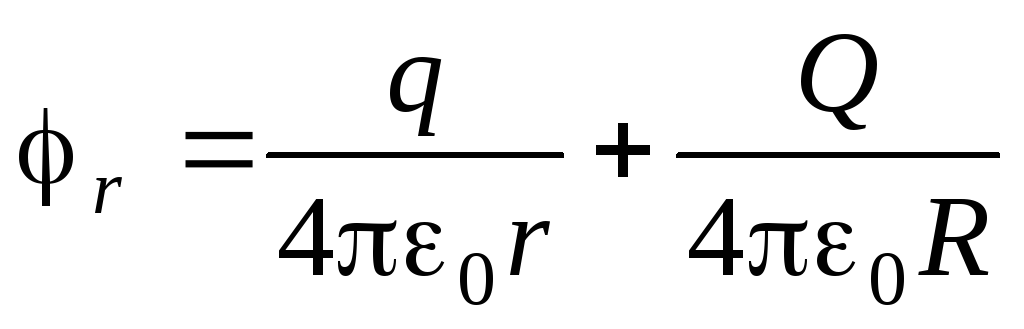
Потенциал сферы радиуса r ,
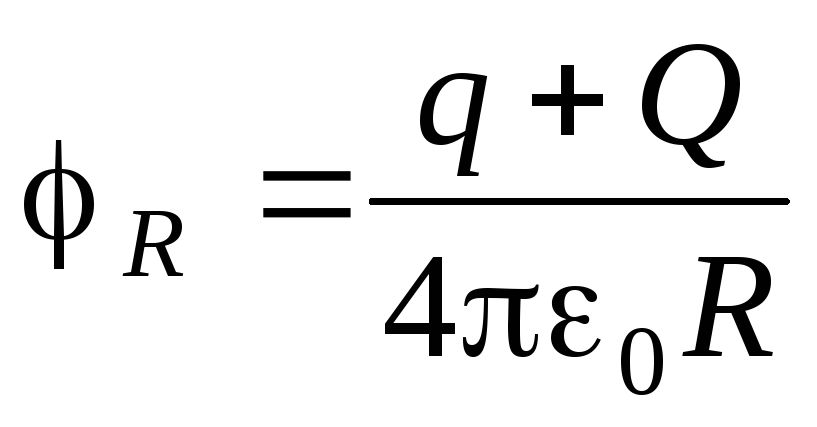
Потенциал сферы радиуса R . При расширении внешней сферы электрические силы совершают работу
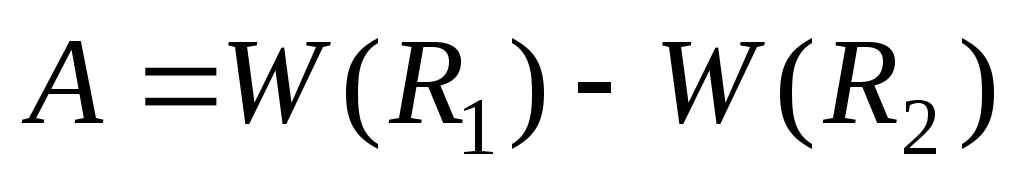 .
.
После подстановок и преобразований получим ответ.
Объемная плотность энергии электрического поля
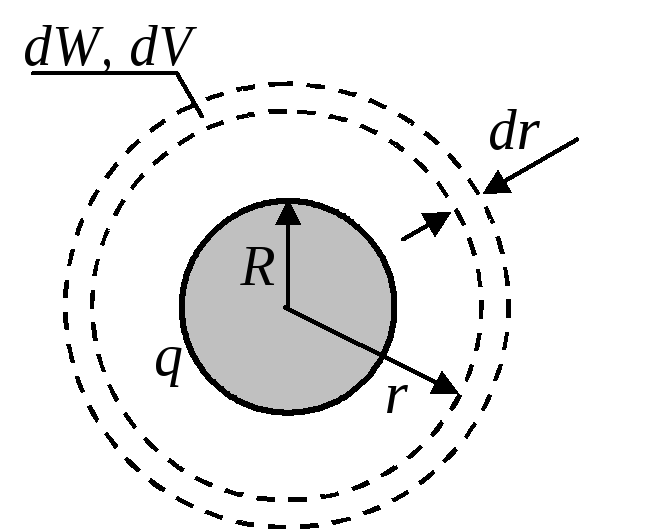
Пример 10 .
Какая часть электрической энергии заряженного проводящего шара, расположенного в вакууме, заключена в пределах концентрической с шаром воображаемой сферы, радиус которой в n раз больше радиуса шара?
Решение .
Объемная плотность энергии электрического поля
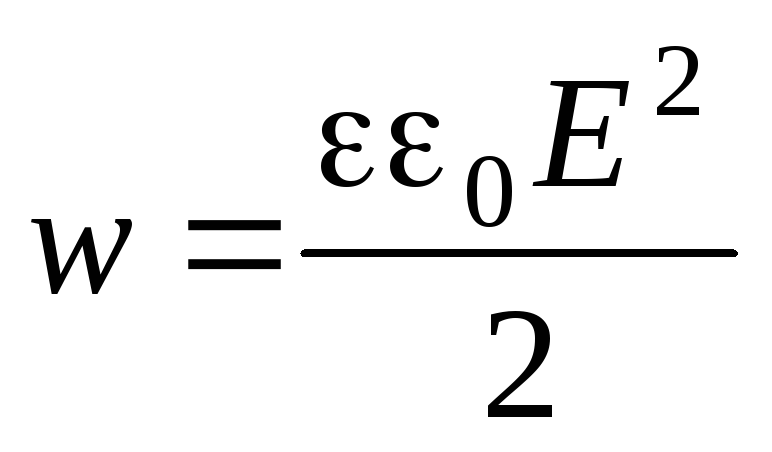
определяет
электрическую энергию
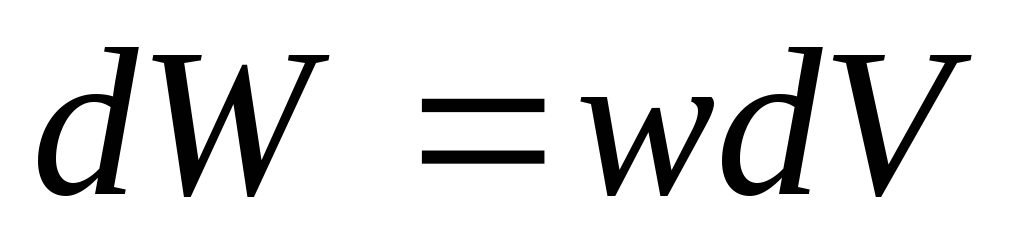 ,
локализованную в бесконечно малом
объеме
,
локализованную в бесконечно малом
объеме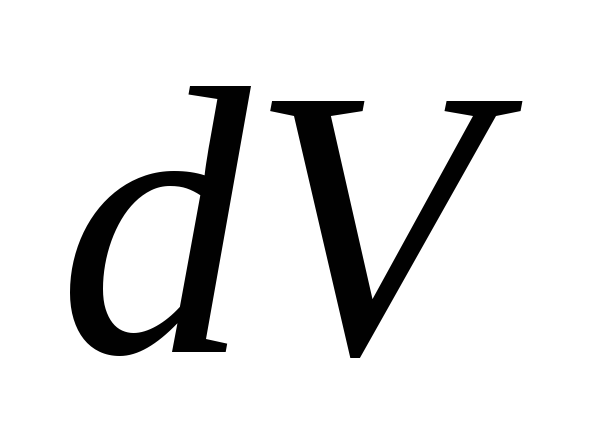 (E
– модуль
вектора напряженности электрического
поля в этом объеме, - диэлектрическая
проницаемость). Чтобы вычислить полную
электрическую энергию заряженного
проводящего шара, мысленно разобьем
все пространство на бесконечно тонкие
шаровые слои, концентрические с заряженным
шаром. Рассмотрим один из таких слоев
радиуса r
и толщины dr
(см. рис.5). Его объем равен
(E
– модуль
вектора напряженности электрического
поля в этом объеме, - диэлектрическая
проницаемость). Чтобы вычислить полную
электрическую энергию заряженного
проводящего шара, мысленно разобьем
все пространство на бесконечно тонкие
шаровые слои, концентрические с заряженным
шаром. Рассмотрим один из таких слоев
радиуса r
и толщины dr
(см. рис.5). Его объем равен
 ,
,
а сосредоточенная в слое электрическая энергия
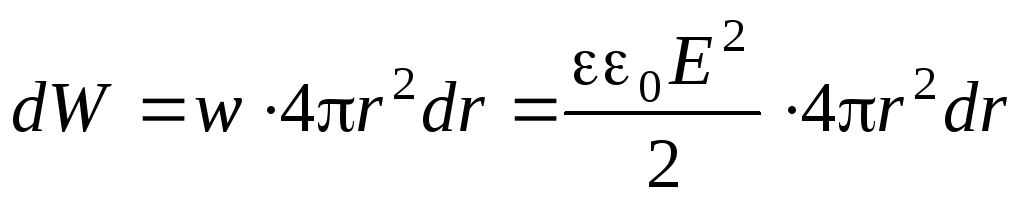 .
.
Напряженность
E
поля заряженного проводящего шара
зависит, как известно, от расстояния r
до центра шара. Внутри шара
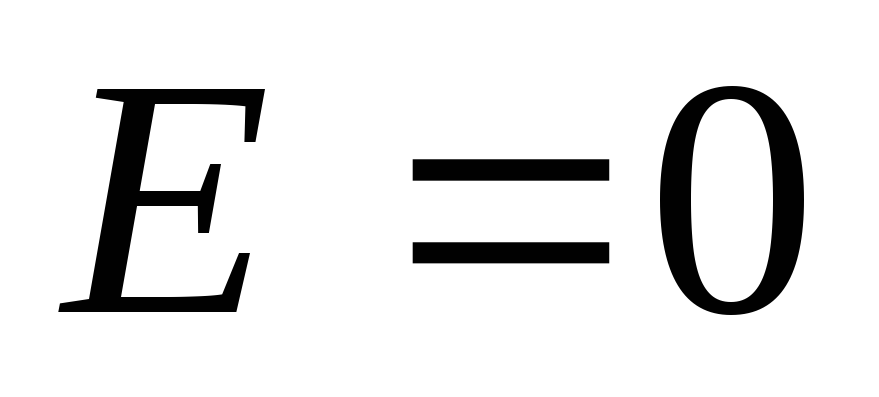 ,
поэтому при вычислении энергии достаточно
рассматривать только те шаровые слои,
радиусr
которых превышает радиус шара R
.
,
поэтому при вычислении энергии достаточно
рассматривать только те шаровые слои,
радиусr
которых превышает радиус шара R
.
При
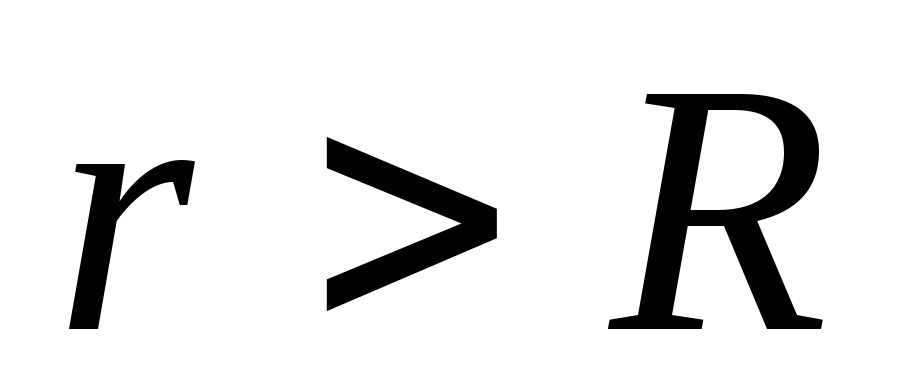 напряженность поля
напряженность поля
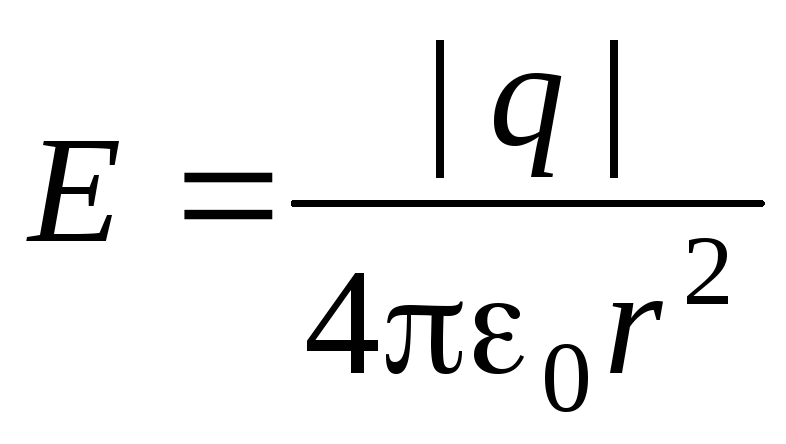 ,
,
диэлектрическая
проницаемость
![]() и, следовательно
и, следовательно
![]() ,
,
где q – заряд шара.
Полная электрическая энергия заряженного шара, определяется интегралом
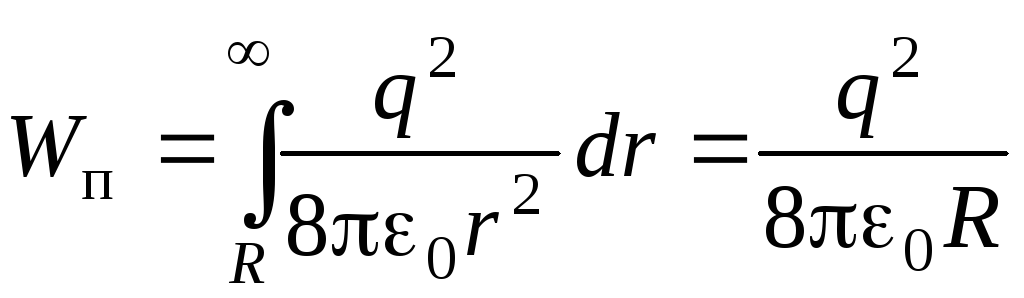 ,
,
а энергия, сосредоточенная внутри воображаемой сферы радиуса nR , равна
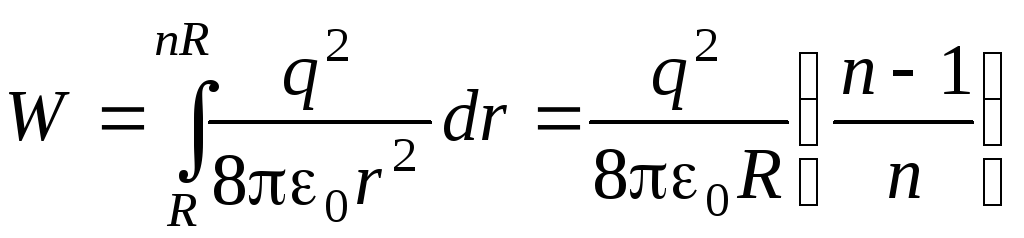 .
.
Следовательно,
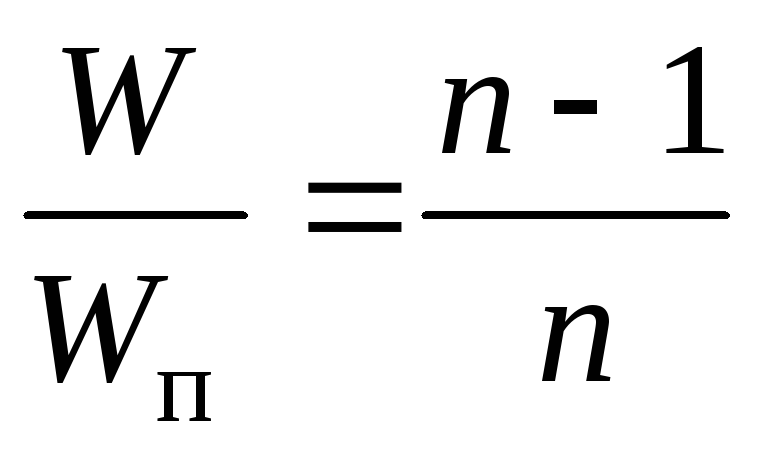 .
.
|
|
|
|
Пример 11.
Определите
электрическую энергию системы, состоящей
из заряженного проводящего шара и
концентрического с ним незаряженного
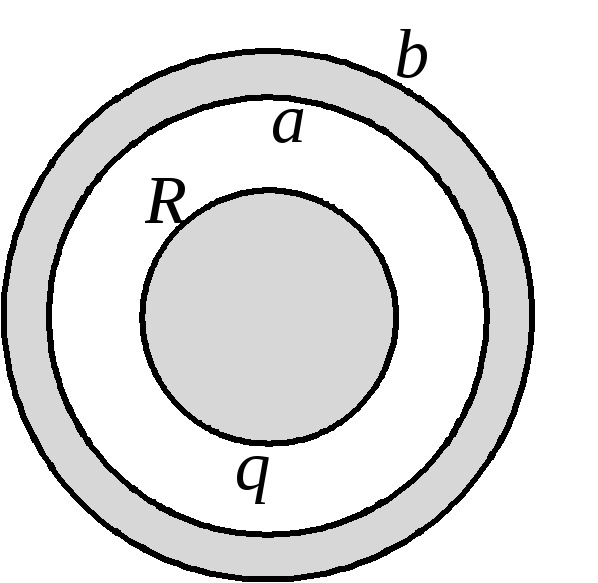
проводящего шарового слоя (рис.6).
Внутренний и внешний радиусы слоя a
и b
,
радиус шара
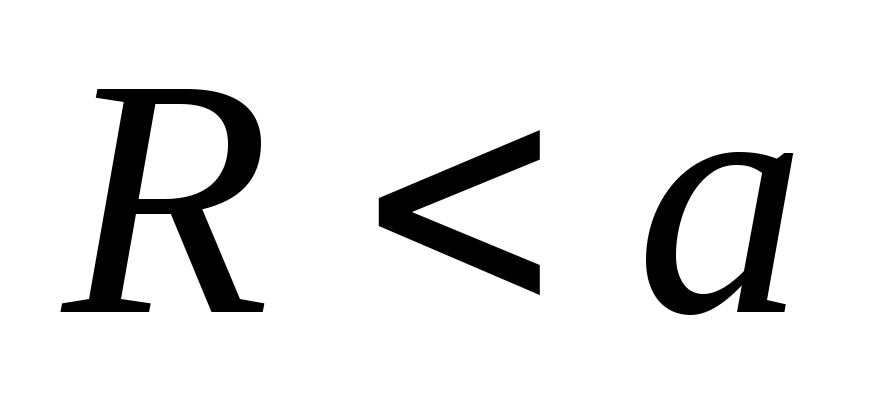 ,
зарядq
,
система находится в вакууме.
,
зарядq
,
система находится в вакууме.
Решение .
На внутренней
и внешней поверхностях шарового слоя
распределены индуцированные заряды.
Их алгебраическая сумма равна нулю,
поэтому индуцированные заряды не создают
электрического поля при
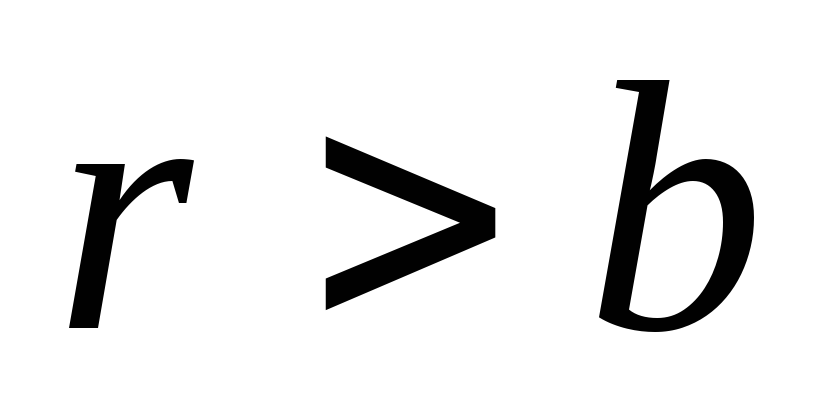 ,
гдеr
– расстояние
от центра системы. В области
,
гдеr
– расстояние
от центра системы. В области
 напряженность поля индуцированных
зарядов также равна нулю, поскольку они
однородно распределены по сферическим
поверхностям. Таким образом, электрическое
поле системы совпадает с полем однородно
заряженной по поверхности сферы, за
исключением внутренней области шарового
слоя, гдеE
= 0.
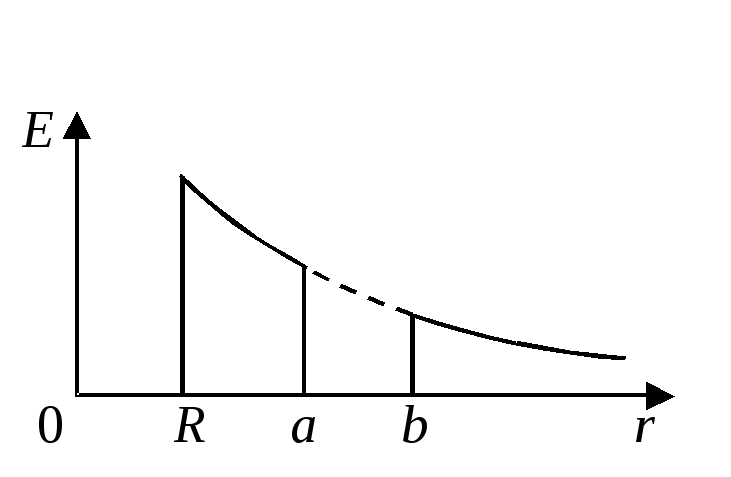
На рис.7 приведен примерный график
зависимости
напряженность поля индуцированных
зарядов также равна нулю, поскольку они
однородно распределены по сферическим
поверхностям. Таким образом, электрическое
поле системы совпадает с полем однородно
заряженной по поверхности сферы, за
исключением внутренней области шарового
слоя, гдеE
= 0.
На рис.7 приведен примерный график
зависимости
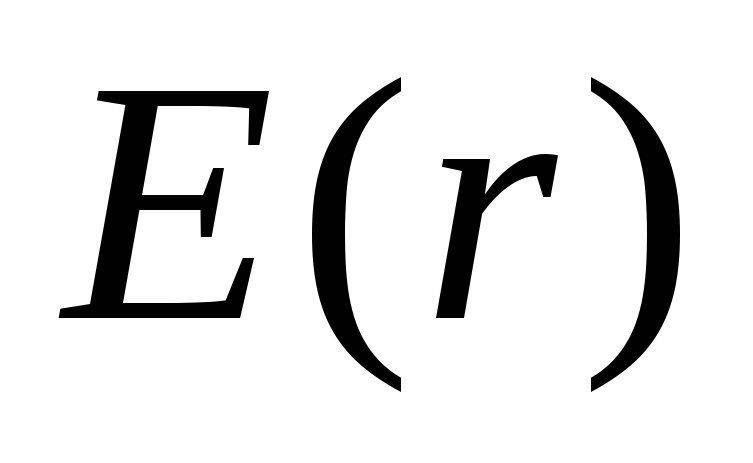 .
Опуская подробные выкладки (см. пример
10), запишем для электрической энергии
системы:
.
Опуская подробные выкладки (см. пример
10), запишем для электрической энергии
системы:
 ,
,
где
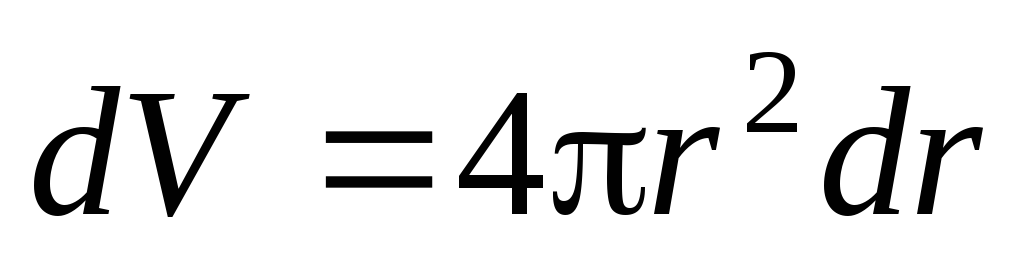 ,
,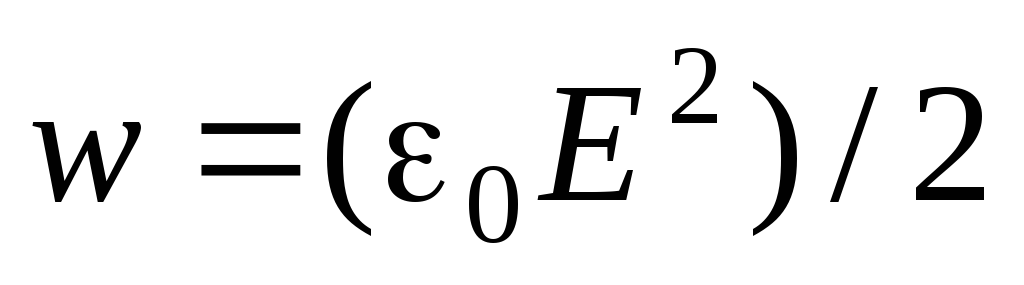 ,
,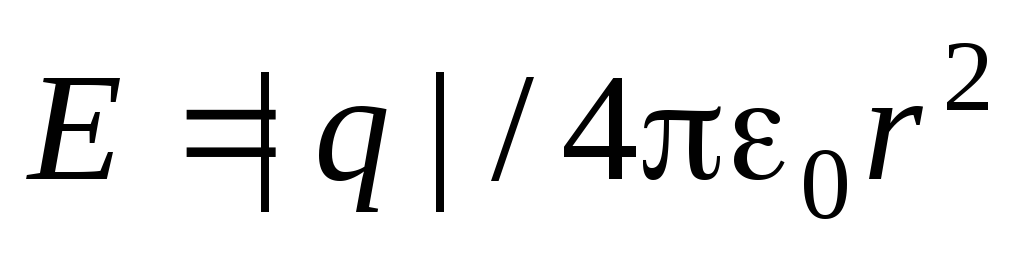 .
После интегрирования получим
.
После интегрирования получим
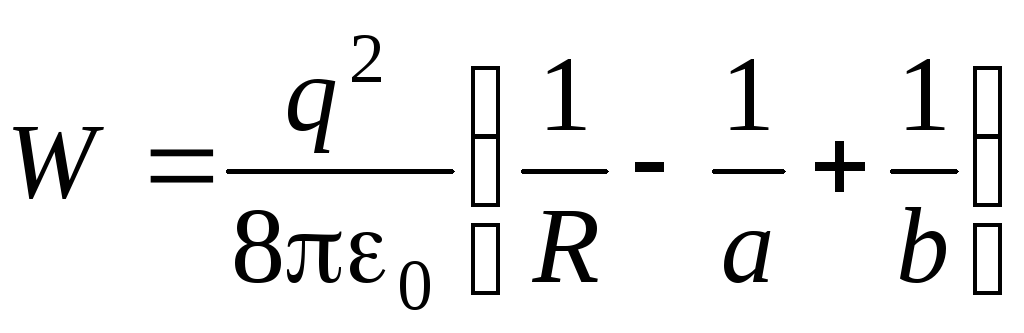 .
.
Пример 12.
Первоначально заряд q распределен однородно по объему шара радиуса R . Затем вследствие взаимного отталкивания заряды переходят на поверхность шара. Какую работу совершают при этом электрические силы? Диэлектрическую проницаемость считайте равной единице.
Решение .
Работа электрических сил равна убыли электрической энергии:
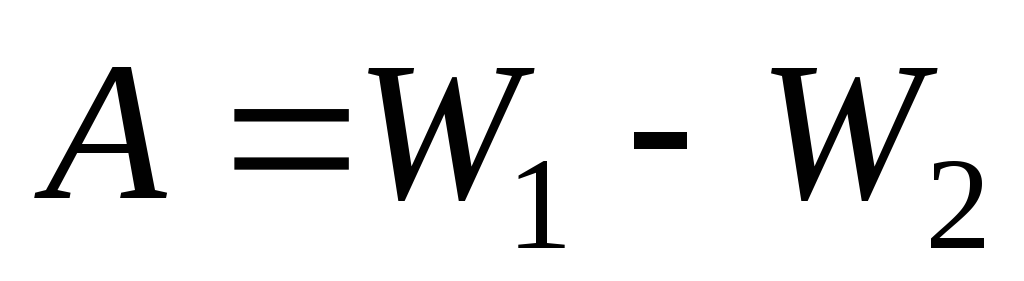 ,
,
где W 1 – электрическая энергия однородно заряженного по объему шара,W 2 – энергия того же шара, однородно заряженного по поверхности. Поскольку суммарный заряд в обоих случаях одинаков, то электрическое поле вне шара при переходе заряда из объема на поверхность не изменяется. Электрическое поле и энергия изменяются только внутри шара.
При помощи теоремы Гаусса можно вывести формулу для напряженности поля внутри однородно заряженного шара на расстоянии r от его центра:
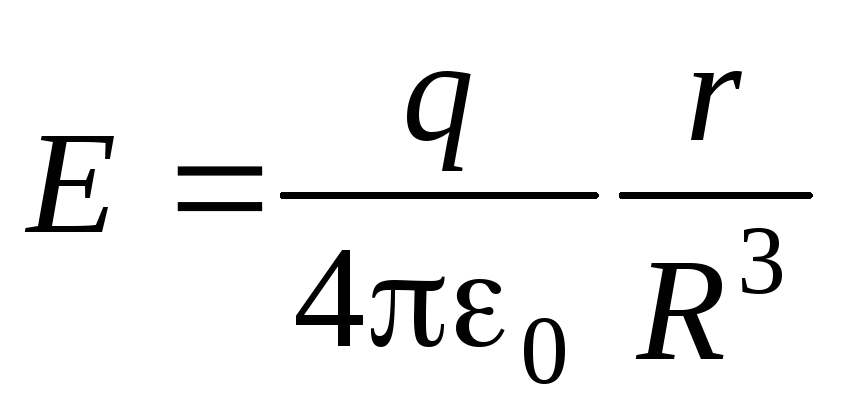 .
.
Электрическая энергия, сосредоточенная внутри шара, определяется интегралом:
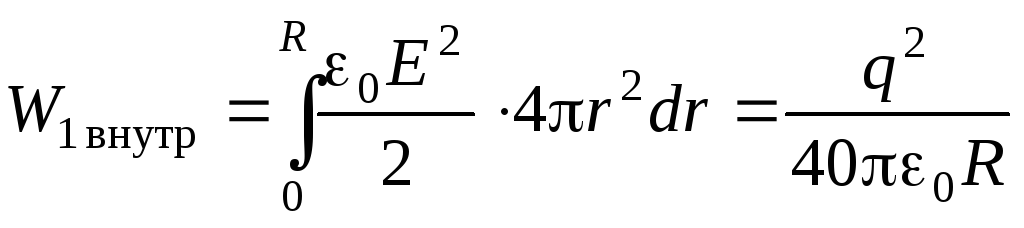 .
.
Когда все заряды перешли на поверхность шара, электрическое поле, а следовательно, и энергия электрического поля внутри шара стали равными нулю. Таким образом,
 .
.
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R . Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 350).
рис. 350
Внутри сферы поле отсутствует. Так, напряженность поля в точке, находящейся на расстоянии r
от центра сферы, равна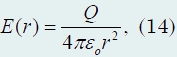
в частности, непосредственно у поверхности сферы, напряженность поля равна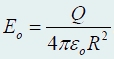 (15)
(15)
Обратим внимание, что произведение S = 4πR 2
есть площадь сферы, тогда отношение
является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе E o = σ/ε o
. Потенциал поверхности сферы также был вычислен нами ранее
Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N
равных малых частей, величины которых равны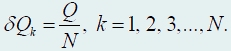
Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N − 1)
зарядами, равен
С использованием симметричной формулы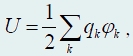
выражение для энергии взаимодействия приобретает вид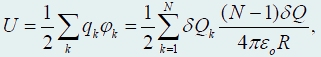
данная сумма содержит N
одинаковых слагаемых, поэтому равна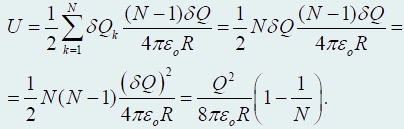
Так как число частей N
, на которые разбивается сфера, может быть сделано сколь угодно большим, то в пределе N → ∞
слагаемое 1/N
исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид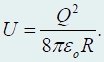
Заметим, что полученное выражение имеет вид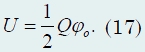
Если сразу заявить, что уменьшение заряда на малую величину δQ
пренебрежимо мало изменяет потенциал сферы, то результат (17) получается прямым применением формулы для энергии взаимодействия зарядов. Однако, обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.
Приведем еще один вывод этой же формулы 1 . Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда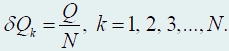
которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того, как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k − 1)
порции заряда, то ее потенциал равен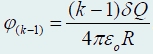
Поэтому для того, что бы перенести на сферу следующую порцию заряда, необходимо совершить работу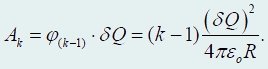
Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии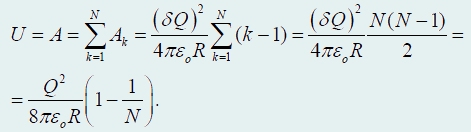
Как и следовало ожидать, мы получили выражение, полностью совпадающее с (17), при бесконечном уменьшении порций переносимых зарядов мы опять приходим к формуле (14).
В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором − энергию, которую необходимо затратить, чтобы собрать их обратно.
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR
, а ее заряд при этом не изменился. Согласно формуле (14), энергия взаимодействия зарядов при этом уменьшится. В пространстве, вне сферы увеличенного радиуса, электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами − исчезло (рис. 351).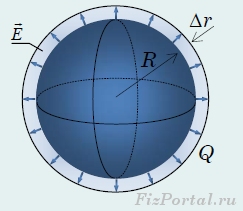
рис. 351
Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя![]()
Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем, запишем в виде
где w
− плотность энергии поля. С другой стороны, эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы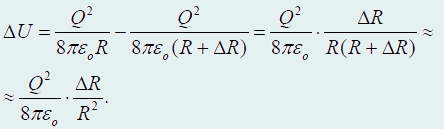
На последнем шаге мы пренебрегли малым изменением радиуса ΔR
. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности![]()
тогда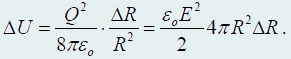
Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой![]()